이 post에서 MAML Family로 많이 언급되는 알고리즘인 FOMAML, Reptile 을 배워보자.
[Arxiv'18] FOMAML: On First-Order Meta-Learning Algorithm
Chelsea Finn 이 ICML'17에서 publish한 Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks 논문의 후속 연구.
논문에 대한 수식보다 Boyang Zhao 이 쓴 post(https://boyangzhao.github.io/posts/few_shot_learning)에 정리되어있는 수식이 더 이해하기 쉬워서 이를 바탕으로 정리.
Motivation
Optimization-based Machine Learning 방법으로 등장한 MAML방법은 다음과 같이 second-order derivatives 를 계산해야 하는 단점 이 있었다.
MAML은 다음과 같이 support set $D^{tr}$ 에 대해 최적화된 task-specific paramter $\phi$ 로 query set $D^{ts}$ 에 대한 loss $\mathcal{L}(\phi, D^{ts})$ 를 계산한뒤, gradient를 $\theta$에 대해 미분해야한다.
이 과정에서, second-order derivatives연산이 필요해지는 데, 본 논문에서 이를 없애고자 함.
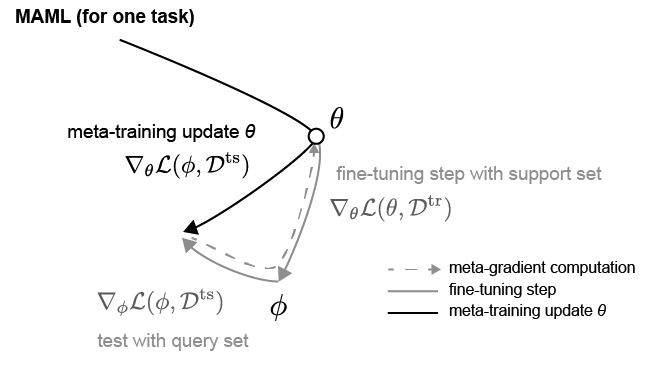
Meta Learning an Initialization: FOMAML
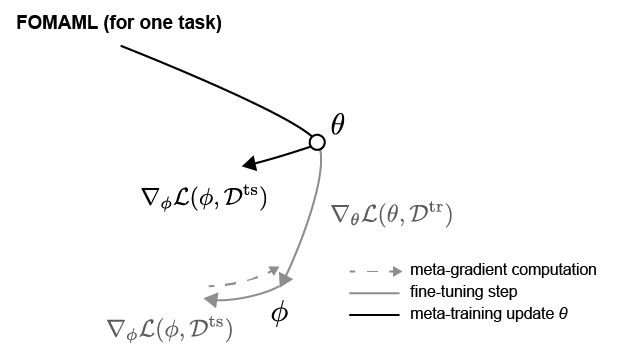
MAML에서 병목이 되는 부분은 다음과 같이 $\nabla_{\theta} \mathcal{L}(\phi, D^{ts})$ 를 계산하는 것이다.
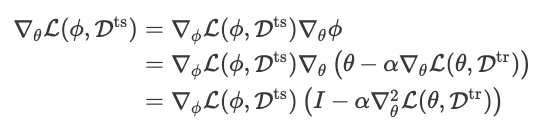
아래와 같이 second-order 를 생략하고, 다음과 같이 approximation 해도, 성능상으로 손해보는것이 크게 없다는게 이 논문의 주장임.
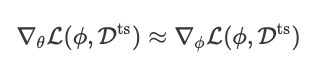
Geometrical 하게 다음과 같은 의미를 지닌다. $\phi$ 에서 query set에 대한 gradient값만을 가져와 $\theta$ 를 업데이트하면 된다.
Reptile
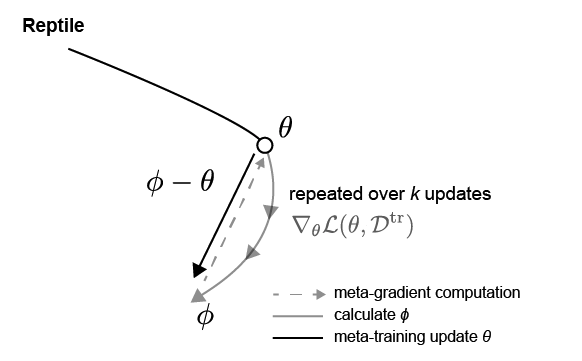
본 논문에서 다른 버전의 first order gradient-based metalearning 방법인 Reptile을 제시하였다. 다음과 같이 $\phi$ 로의 변화량만큼을 업데이트 해준다.
이때 주의사항은 k > 1 (2 이상) 업데이트를 해준 $\phi = \phi_k$ 라는 것이다. 그리고, 이 방법은 전처럼 support set이 필요없다.
구체적인 알고리즘은 다음과같다.

sinusoid 데이터에서 MAML기반으로 evaluation(새로운 task에 대해 $k$ 번의 업데이트를 통해 $\phi_k$를 구해 평가)을 해보면 다음과 같이 $k$가 커질수록 새로운 task에 잘 적응하는 모습을 보인다.
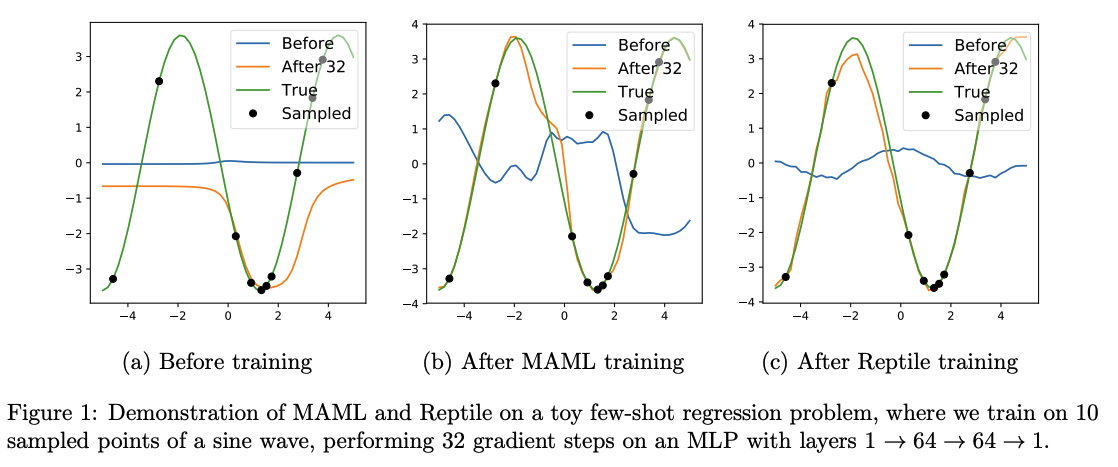
Experiments
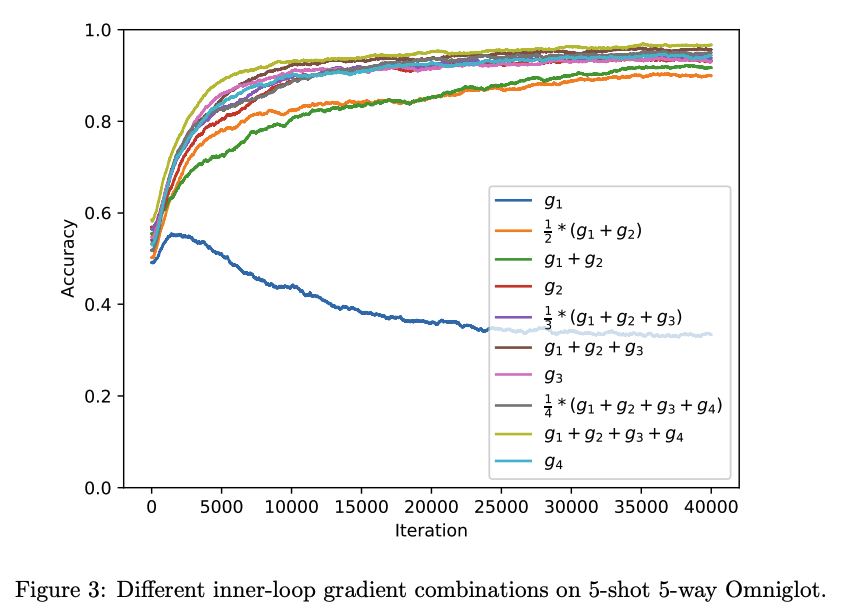
Reptile 에서 k > 1 로 쓰라는 이유가 이 실험에서 명확히 보인다. inner-loop의 $k$번째 iteration에서 발생하는 gradient를 $g_k$ 라 하였을때, 파라미터를 업데이트에 이용된 gradient 누적값에 대한 경우를 나눠 실험 결과를 보면 다음과 같이 $g_1$을 제외하고는 성능이 잘 오르는 것을 알 수 있음.