Background
추천 모델의 다음의 cummulative discounted reward를 maximize 하는게 목표다.
$$
\underset{\theta}{max}{\mathcal{J}{\pi}(\theta)} = \underset{\theta}{max}{\mathbb{E}{\tau \sim \pi(\theta)}[R(\tau)]}
, R(\tau) = \sum_{0}^{\vert \tau \vert} \gamma^t r(s_t, a_t)
$$
REINFORCE with Off-Policy Correction
$$
\begin{align}
\nabla_{\theta} \mathcal{J}(\theta)
&= \sum_{s} d_{\pi_{\theta}}(s) \sum_{a} \nabla_{\theta} \pi_{\theta}(a \vert s) Q_{\pi}(s, a) \\
&= \sum_{s} d_{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(a \vert s) \frac{ \nabla_{\theta} \pi_{\theta}(a \vert s)}{\pi_{\theta}(a \vert s)} Q_{\pi}(s, a) \\
&= \textcolor{pink}{ \sum_{s} d_{\pi_{\theta}}(s) \sum_{a} \pi_{\theta}(a \vert s)} \nabla_{\theta} log \pi_{\theta}(a \vert s) Q_{\pi}(s, a) \\
&= E_{\pi_{\theta}} \left[ \nabla_{\theta} log \pi_{\theta}(a \vert s) Q_{\pi}(s, a) \right]
\end{align}
$$
Monte Carlo 근사 적용
$$
\begin{align}
\nabla_{\theta} \mathcal{J}(\theta)
& \simeq \nabla_{\theta} log \pi_{\theta}(a \vert s) Q_{\pi}(s, a) \\
& \simeq \nabla_{\theta} log \pi_{\theta}(a \vert s) R(s, a) \\
R_t(s_t, a_t) &= \sum_{t' = t}^{\vert \tau \vert} \gamma^{t' - t} r(s_t', a_t')
\end{align}
$$
Off-Policy
행동하는 policy와 학습하는 policy가 분리되어 있다.
| behavior policy |
learned policy |
| $\beta$ |
$\pi_{\theta}$ |
Importance sampling 기법을 이용
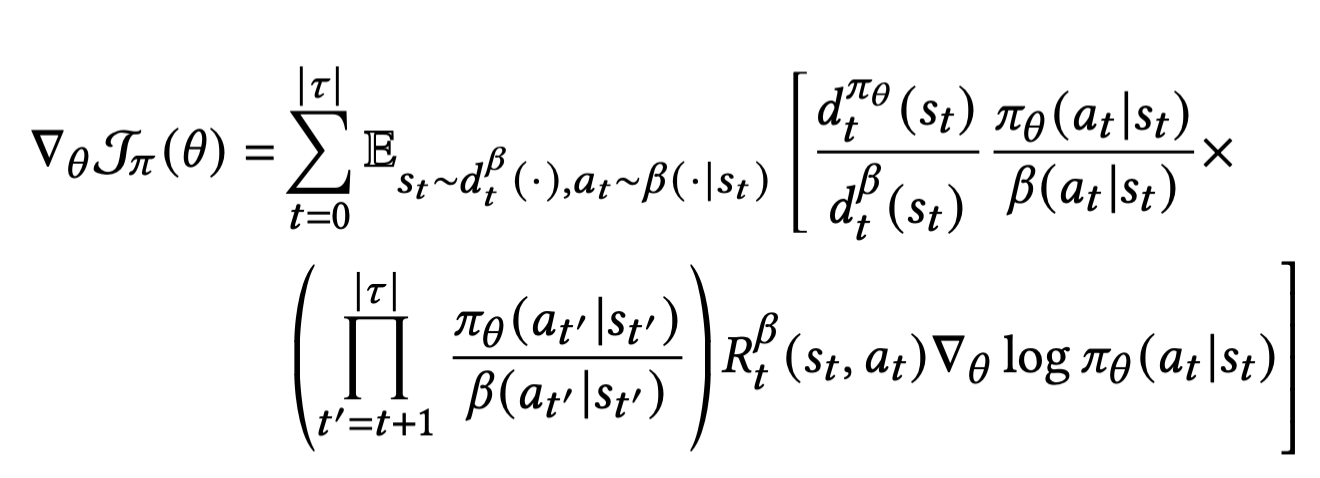
Future trajactories 에 대한 Impantance weight를 무시하는 first order approximation 적용[*]
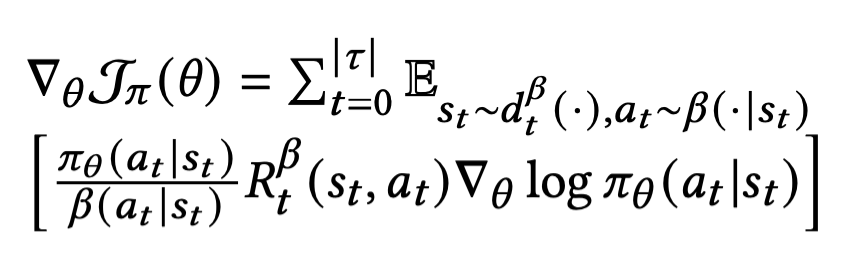
[*] Top-K Off-Policy Correction for a REINFORCE Recommender System, WSDM 2019
Off-Policy Actor-Critic
Actor
위의 REINFORCE에 사용한 손실함수에서 reward 를 Q 함수로 대체하여 policy(actor) 네트워크의 Loss
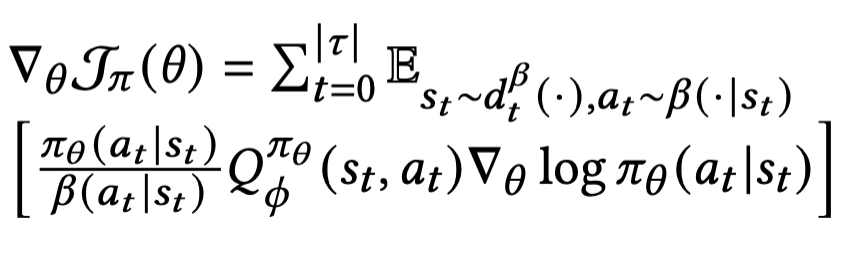
Ctric
MDP 가정으로부터 나온 Bellman Equation을 생각
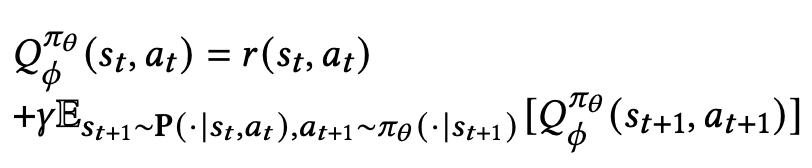
위의 Recurrence 를 수렴하게 하기 위한 target(critic) 네트워크의 MSE Loss
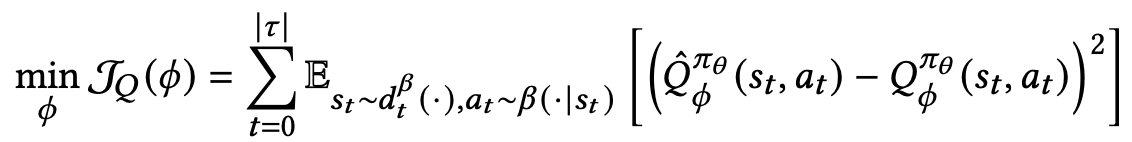
논문에서는 MSE와 MAE를 혼합한 Huber loss를 사용함. Outlier에 민감한 MSE를 보완함.
Estimating Target
Target label은 일반적으로 다음과 같이 구함.
하지만, 본 논문에선 두 가지 방식 사용
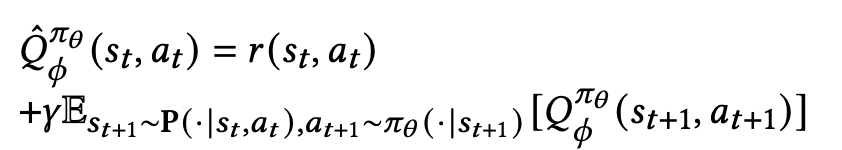
이해를 돕기 위해 표현 방식 설명
Importance Sampling with Behavior policy
$a_{t+ 1} \sim \beta(\cdot \vert s_{t + 1})$
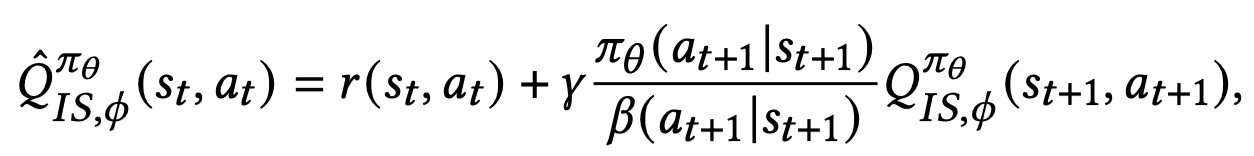
- 장점
- Importance weight의 보정 효과로 $Q$의 예측이 정확해짐
- Importance wieght를 곱하는 것이므로 unbiased ($\beta \rightarrow 0, \pi \rightarrow 0$)
-
$a_{t+ 1} \sim \beta(\cdot \vert s_{t + 1})$ 이기 때문에 유저 피드백을 가져와 활용할 수 있음
- 단점:
-
$\pi$ 와 $\beta$의 차이가 있고, $\beta$ 분포에 의해 뽑힌 action 샘플에 의존하기 때문에 variance 가 큰 편
-
$\beta$가 선택하지 않은 action 을 $\pi$ 가 선택할 수 있기 때문에 $\pi$입장에서 value를 under-estimate 할 수 있음 (deficient support[*])
[*]: Off-policy Bandits with Deficient Support, SIGKDD 2022
Sampling with Learned policy
$a_{t+ 1}^{'} \sim \pi_{\theta}(\cdot \vert s_{t + 1})$
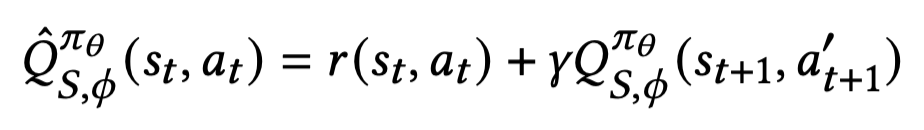
- 장점
-
$a_{t+1}^{'}$를 여러번 샘플링 할 수 있기 때문에 $Q_{S}^{\pi}$ 를 평균내 variance를 줄일 수 있다.
- 단점
- Importance weight를 사용한 보정효과가 없어 $Q$ 예측 정확도가 낮음
-
$\beta$가 뽑지않은 action의 경우에 유저의 피드백 활용을 할 수 없음(logged data안에 존재하지 않으므로)
Sampled Softmax
Softmax를 계산할때 action space가 너무 크면 사이즈를 줄여 샘플링을 한 action space에서 계산함. 이때 global action space보다 작은 action space를 뽑기 위한 Candidate space $C$를 어떤 global categorical distribution $\mu$등을 가정하여 뽑는다. $\pi$, $\beta$등 계산에서 쓰임.
Architecture
| Loss 종류 |
Network |
Loss 종류 |
| $J_{\pi}$ |
Actor for learned policy |
Cross Entropy |
| $J_{\beta}$ |
Actor for behavior policy |
Cross Entropy |
| $J_{Q}$ |
Critic (Target) |
Huber Loss |
| $\mathcal{R}_{\pi}$ |
Entropy Regularizer[1] for confidence penalty |
Hinge Loss |

오타: 그림에 $J_{\theta}$ 를 $J_{\beta}$로 수정
휴리스틱한 방법으로 sampled softmax기법과 boltzmann exploration 기법[2] 사용
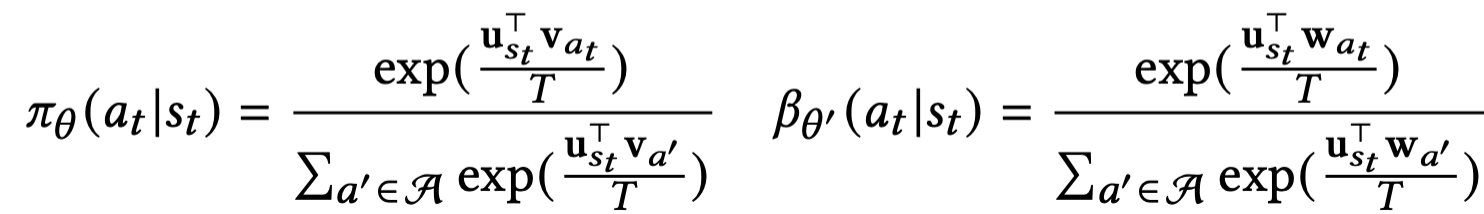
[1]: Regularizing Neural Networks by Penalizing Confident Output Distributions, ICLR 2017
[2]: Cortical substrates for exploratory decisions in humans, Nature 2006
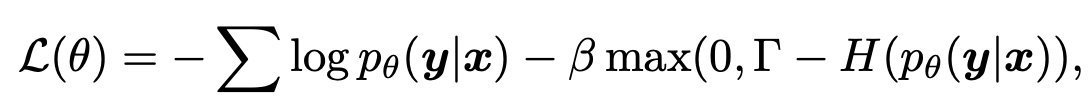
Experiments
Dataset
- Reward는 scalar 값: user feedback/experience, such as engagement, responsibility,satisfaction 등을 이용
Offline Experiments
- Trajactory 중 1% 는 evaluation으로 이용
- Aaction space는 가장 최근 1000만개 아이템들
- 매 gradient update 마다 batch size 는 1024 user trajactories (6시간 내의 윈도우에서)
Importance of Features
노랑: User state & context feature
초록: + time delta
보라: + novelty
마젠타: + immedidate reward
[a]와는 [b-d]에서 상반된 결과를 보임
policy network with the least expressive critic outputs a policy that resembles the behavior policy the most
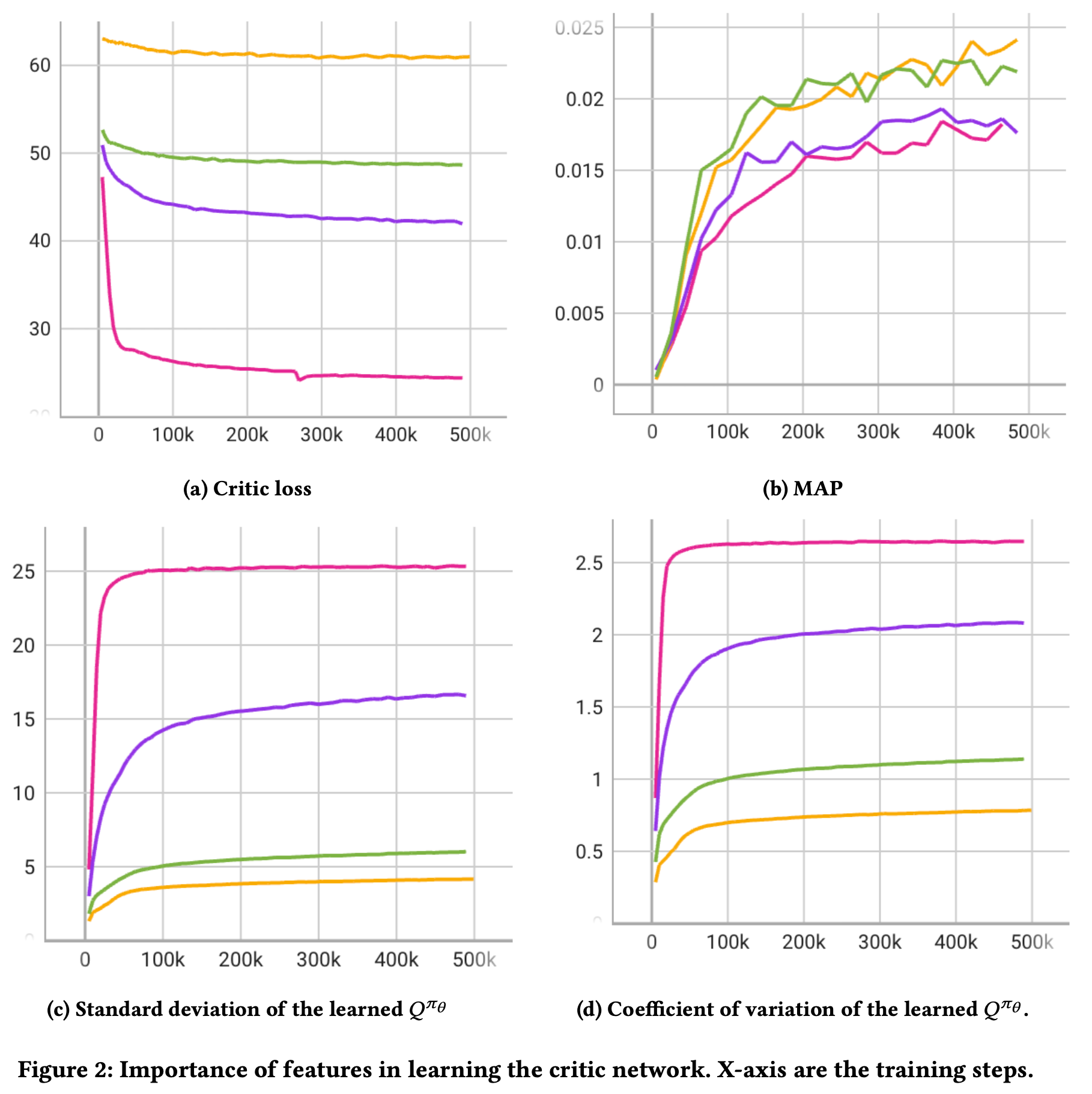
Q 값의 사용
REINFORCE[*] 를 Baseline으로 사용 (cumulative reward를 Q대신 사용)
[a]: 업데이트 수가 많아질수록 less popular
[b]: immediate feedback보다는 future reward에 치중하다보니 immediate는 작아진 결과를 보임 (의문: 약간 변명같이 느껴짐 immediate도 늘면서 future도 늘 수 있지 않은가?)
[c]: weak causual relation (negative)
[d]: noisier
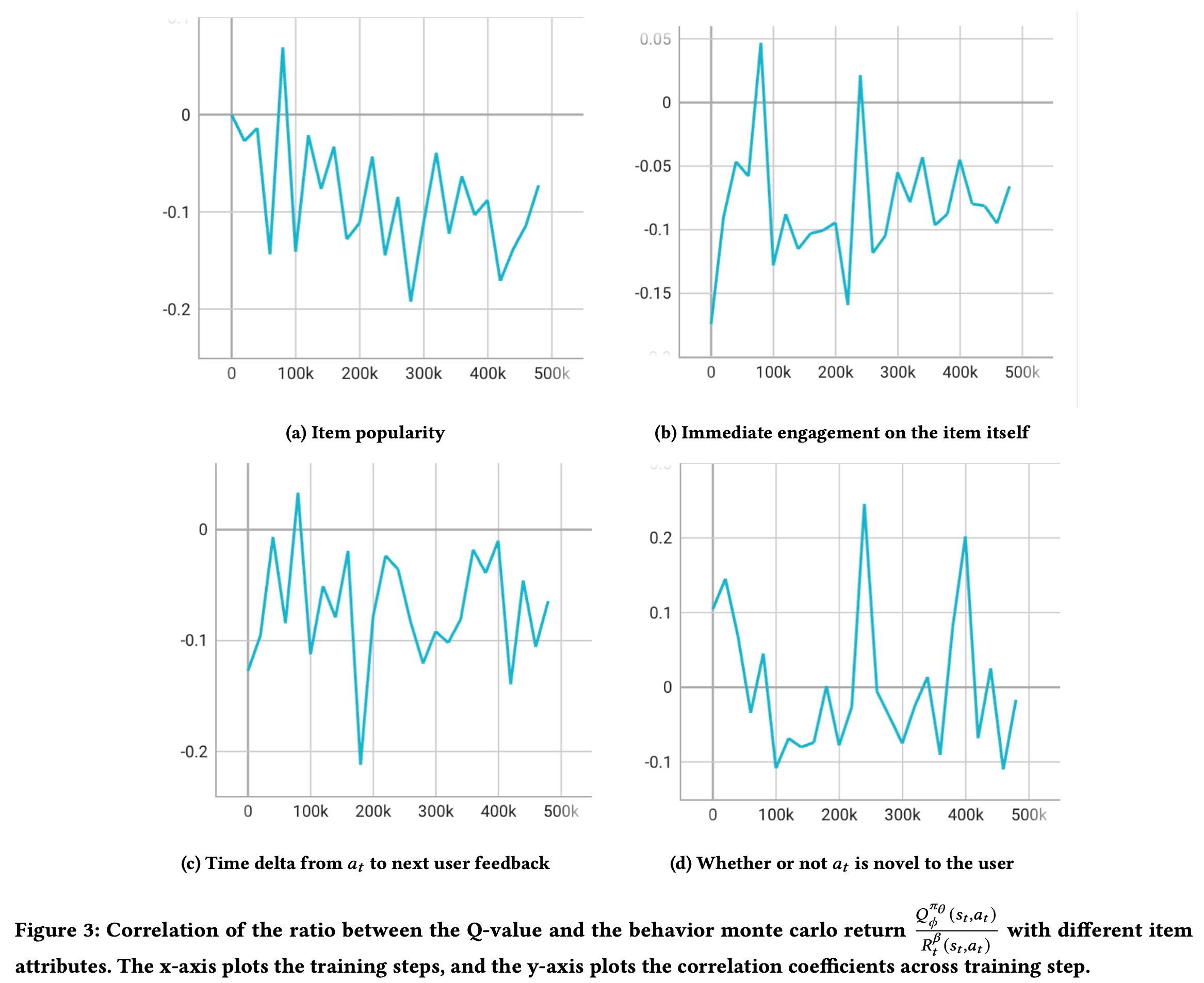
[*] REINFORCE(NIPS 1999, Richard S. Sutton)
Online Experiments
A/B 테스트
여러 도메인(구체적으로 밝히지 않음) 에서 유저당 백만개중 수백개의 아이템을 뽑고 ranking을 해서 유저에게 보여줌(2 stage인것으로 보임). 대조군은 REINFORCE 알고리즘. 4주동안 진행.
[a]: +0.07% 향상 (이게 큰값인가 봄)
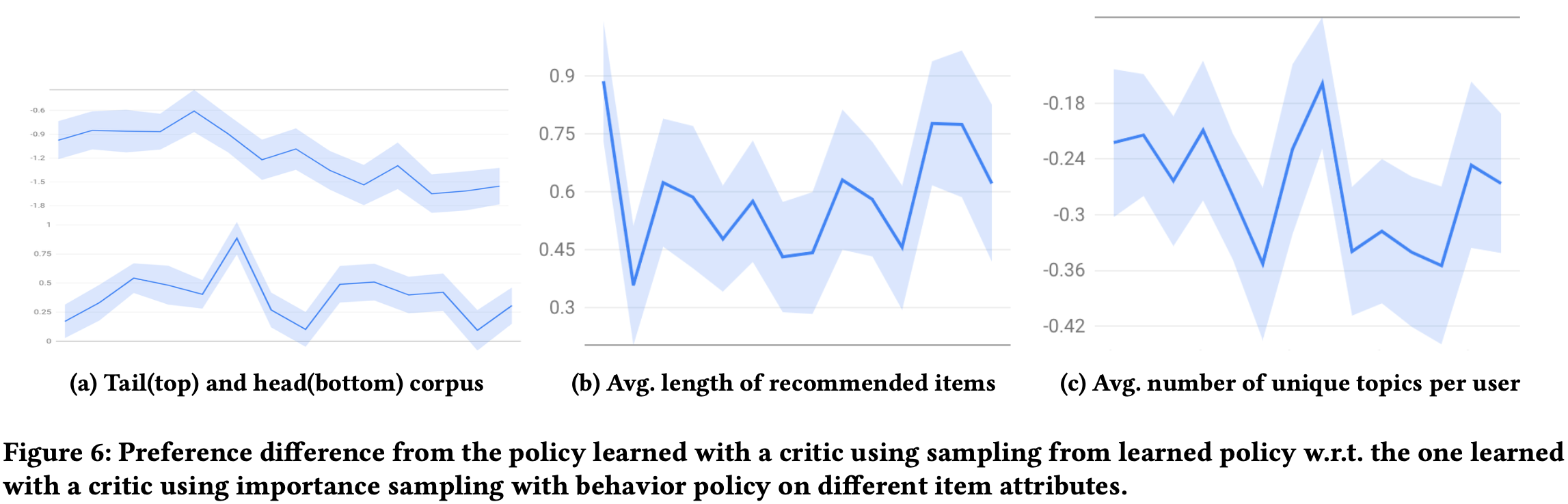
[b]: tail corpus는 증가, head는 감소 (Figure 3[a]에서 보이듯 인기 아이템이 줄은 것으로 보아 유사한 양상을 보임)
[c]: (의견:Figure3[b]에서 immediate engagement 가 줄었기 때문에 더 짧은 컨텐츠를 추천한거 라고하는데 납득하기 어렵다.)
[d]: 확실히 새로운 토픽을 더 추천해주는 경향이 있음
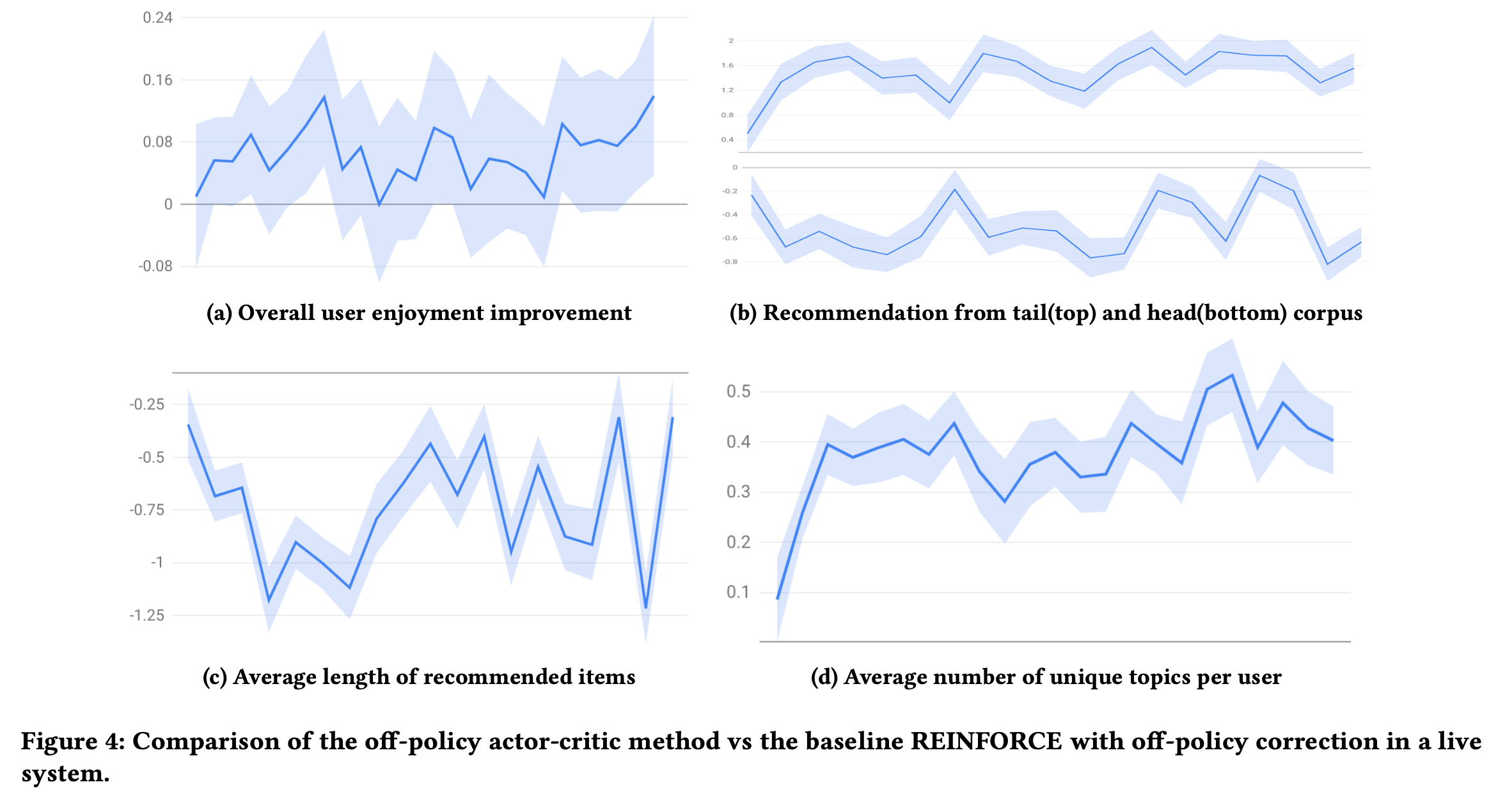
Ablation Study
2주동안 진행
[a]: Target network를 도입하였을때 소정의 향상이 있음 (의견: 더 향상하지 못한건 batch size가 너무 크고, $\gamma$가 너무 작다고 헀는데 이건 핑계인 것 같고 바꾸어 가면서 비교해보았으면 되지 않았나 생각이듦.)
[b]: (약간 헷갈리는데) 파란색선이 유저 피드백을 뺀 그래프인 것 같고, 역시 제거하니 성능이 약간 낮음. 유저 피쳐를 풍부하게하는게 좋다.
[c]: 정확한 비교를 위해 유저의 응답 피쳐를 제거했고 (그래서 음수 쪽 그래프임), 파란것은 $\hat{Q}_{IS}$, 빨간것은 $\hat{Q}_S$인데 확실히 IS를 쓰는게 좋음
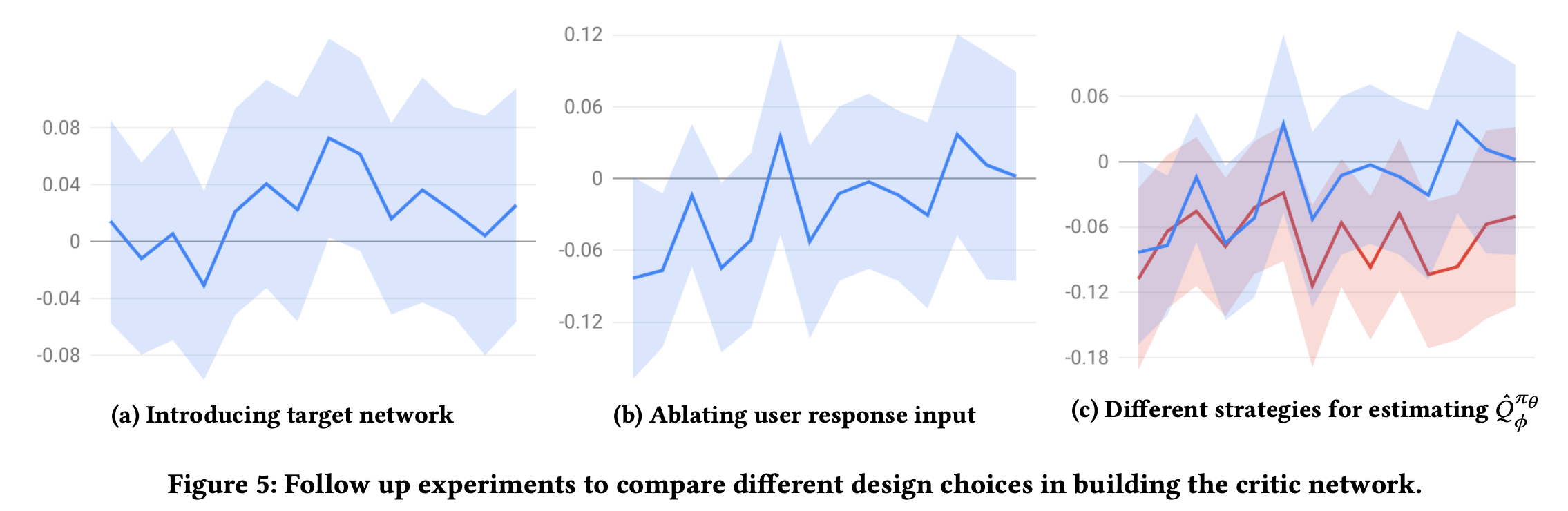
Importance Sampling On/Off
$\hat{Q}_{IS}$대비 $\hat{Q}_S$를 사용한 방식을 그래프로 표현
결과를 보면 IS를 사용하지 않으면 더 근시안적(myopic)인 policy가 됨.
Softmax Policy Induces Pessimism
Offline RL 계열에서 문제가 되는 개념인 Out Of Distribution, OOD 라는 개념이 있음.
이것은 behavior policy에서 보지못한 action이 learned policy에서 선택되는데 under-estimate되는 문제.
즉, 아래 수식에서 $a_{t+1}^{'} \sim \pi_{\theta}(\cdot \vert s_{t+ 1})$가 $\beta$에서 뽑히지 않은 item이면 발생하는 문제.
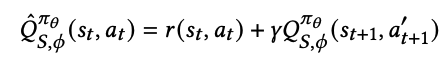
이 문제에 대한 해결론으로 Entropy Regularization Term인 $\mathcal{R}_{\pi}(\theta)$가 Loss 에 포함되어 있는데, 추가적인 방법을 제안하거나 실험을 하지는 않았고 Future work로만 제시 함.
Conclusion
- Actor-Crtic 모델을 제시하였고, 기존 REINCEFORCE와 Offline/Online에서 비교 & 분석 함.
- 약간의 성능 향상과, 여러 분석을 통한 방법론의 차이를 설명
- Softmax Policy 가 pessimism을 유발함을 밝힘. (의견: 하지만 검증이 부족함)